Las Sucesiones.
Una sucesión, es un conjunto de varios elementos (pudiendo ser letras, números o figuras), uno detras de otro, que tienen una secuencia a la vez que mantienen un orden, siguiendo reglas establecidas
Tmbién podemos definirla como, una sucesión es un conjunto ordenado de números, donde cada número sigue un patrón o regla específica. En otras palabras, es una serie de números dispuestos en un orden determinado, donde cada número se relaciona con los anteriores siguiendo una regla o patrón establecido.
En una sucesión, cada número individual se conoce como un término. Estos términos están dispuestos en un orden específico, lo que significa que el primer término viene antes del segundo, el segundo antes del tercero, y así sucesivamente. La importancia de este orden radica en la relación que existe entre los términos consecutivos.
Lo que hace que una sucesión sea interesante es la regla o patrón que determina cómo se generan los términos. Esta regla puede ser muy simple, como sumarle una cantidad fija a cada término anterior, o más compleja, como una fórmula matemática. En cualquier caso, esta regla nos permite predecir o calcular cualquier término de la sucesión, siempre y cuando conozcamos los términos anteriores y entendamos cómo se aplica la regla.
Por ejemplo, en la sucesión 2, 4, 6, 8, 10, ..., cada término se obtiene sumando 2 al término anterior. En la sucesión 1, 3, 9, 27, 81, ..., cada término se obtiene multiplicando por 3 al término anterior. Estos son solo dos ejemplos simples, pero las sucesiones pueden ser mucho más variadas y complejas.
Elementos de una sucesión
Una sucesión está compuesta por varios elementos clave que nos ayudan a entender su estructura y comportamiento. A continuación, describiremos cada uno de estos elementos:
- Términos: Los términos son los números individuales que conforman la sucesión. Cada término ocupa una posición específica en la sucesión y sigue un orden determinado.
- Término inicial: El término inicial es el primer número de la sucesión. Es el punto de partida desde el cual se construye la secuencia. Este término nos proporciona información sobre el comienzo de la sucesión.
- Término general: El término general es una fórmula matemática que nos permite calcular cualquier término de la sucesión sin necesidad de conocer todos los términos anteriores. Esta fórmula puede depender de la posición del término en la sucesión o de otras variables.
- Regla de formación: La regla de formación es el patrón o la regla que sigue la sucesión para obtener cada término a partir del anterior. Esta regla puede ser una operación matemática simple, como sumar o restar una cantidad fija, o una fórmula más compleja que involucre operaciones más elaboradas.
Entender estos elementos es clave para comprender cómo se construye y se comporta una sucesión. Nos permiten predecir los términos futuros, calcular la suma de los términos y explorar las propiedades matemáticas de la secuencia.
Tipos de sucesiones
Las sucecioenes pueden clasificarse en diferentes tipos según las características de su formación. A continuación, exploraremos los tipos principales de sucesiones:
Numéricas
Geométricas
Aritméticas
Literales
Alfanuméricas
Gráficas
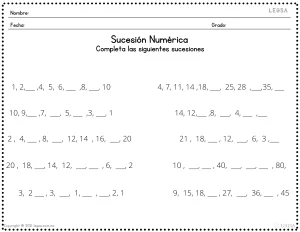
Ejemplo de Actividades imprimibles
Las sucesiones son un concepto fundamental en matemáticas y
Sucesión numérica.
Una sucesión numérica, es un conjunto de varios números, uno detrás de otro, que tienen una secuencia a la vez que mantienen un orden, siguiendo reglas establecidas- Las sucesiones numéricas pueden ser para adelante, hacia atrás, alternadas o alternas.
Ejemplos.
Sucesiones para adelante: (7,8,9,10)
Sucesiones para atrás: (10,9,8,7)
Sucesiones alternadas: (3,6,9,12)
Sucesiones alternas: (1,2,1,2)
Sucesiones geométricas.
En este tipo de sucesiones, cada término se obtiene multiplicando el término anterior por una constante fija llamada razón. Esto significa que la relación entre términos consecutivos es de multiplicación.
Por ejemplo, la sucesión 2, 6, 18, 54, ... es una sucesión geométrica, ya que cada término se obtiene multiplicando el término anterior por 3.
Sucesiones aritméticas.
En una sucesión aritmética, cada término se obtiene sumando una constante fija llamada diferencia al término anterior. Esto crea una progresión aritmética en la que la relación entre los términos consecutivos es de adición.
Por ejemplo, la sucesión 3, 7, 11, 15, ... es una sucesión aritmética, ya que cada término se obtiene sumando 4 al término anterior.
Sucesión literal.
Una sucesión literal, es un conjunto de varias letras, una detrás de otra, que tienen una secuencia a la vez que mantienen un orden, siguiendo reglas establecidas.
Ejemplos.
A,B,C,D
g, k, g, k, g, k
A, A, A, B, B, B, C, C, C
x, o, j, x, o, j
Sucesión alfanumérica.
Una sucesión alfanumérica, es un conjunto de varias letras y números, unos detrás de otros, que tienen una secuencia a la vez que mantienen un orden, siguiendo reglas establecidas.
Ejemplos.
a, 1, b, 2, c, 3
F, G, 4, 1, F, G, 4, 1
Sucesión gráfica.
Una sucesión gráfica, es un conjunto de varias figuras, unas detrás de otras, que tienen una secuencia a la vez que mantienen un orden, siguiendo reglas establecidas.
Ejemplos.
■, ▲, ●, ■, ▲, ●
◆, ▰, ▮, ◆, ▰, ▮

Ejemplo de Actividades imprimibles
Características Básicas de las Sucesiones
| Característica | Descripción |
|---|---|
| Orden | Las sucesiones son conjuntos ordenados de números, lo que significa que cada término ocupa una posición específica en la secuencia. |
| Patrón o regla | Cada término de la sucesión sigue un patrón o una regla específica que determina cómo se genera a partir del término anterior. |
| Términos | Están compuestas por términos individuales, que son los números que conforman la secuencia. |
| Término inicial | Es el primer número de la sucesión, el cual da inicio a la secuencia y proporciona información sobre su comienzo. |
| Término general | Es una fórmula matemática que nos permite calcular cualquier término de la sucesión sin necesidad de conocer todos los términos anteriores. |
| Regla de formación | Es el patrón o la regla que sigue la sucesión para obtener cada término a partir del anterior. Esta regla puede ser simple o compleja, dependiendo del tipo de sucesión. |
Aplicaciones Prácticas de las Sucesiones
Los conceptos y principios relacionados con las sucesiones tienen aplicaciones prácticas en varios campos de estudio y en situaciones cotidianas. A continuación, exploraremos algunas de estas aplicaciones:
- Secuencias de números en computación: En informática, las sucesiones son utilizadas en algoritmos y programas para generar secuencias de números que siguen ciertos patrones. Por ejemplo, en la generación de números pseudoaleatorios, se utilizan sucesiones para producir secuencias de números que se comportan de manera aparentemente aleatoria pero que siguen una regla predefinida.
- Progresiones en finanzas: En el ámbito financiero, las sucesiones aritméticas y geométricas son utilizadas para modelar el crecimiento de inversiones, préstamos o deudas a lo largo del tiempo. Por ejemplo, al calcular los intereses compuestos sobre un préstamo, se puede usar una sucesión geométrica para determinar cómo crece la deuda con el tiempo.
- Series numéricas en ciencias naturales: En disciplinas como la física o la biología, las sucesiones y series numéricas son utilizadas para modelar fenómenos naturales y realizar predicciones. Por ejemplo, en la física, las sucesiones aritméticas pueden utilizarse para representar el movimiento uniformemente acelerado de un objeto, mientras que las sucesiones geométricas pueden modelar el crecimiento exponencial de una población.
- Patrones en el arte y la música: En el arte y la música, las sucesiones pueden ser utilizadas para crear patrones y estructuras interesantes. Por ejemplo, en la composición musical, se pueden utilizar sucesiones aritméticas para crear ritmos repetitivos, o sucesiones geométricas para crear variaciones en la melodía.
Estas son solo algunas de las muchas aplicaciones prácticas de los conceptos de sucesiones en diversos campos de estudio y en la vida diaria. Comprender cómo funcionan las sucesiones y cómo aplicar sus principios puede ser útil en una amplia gama de situaciones y profesiones.
Ideas de Actividades para practicar sucesiones
Practicar con sucesiones es una excelente manera de fortalecer la comprensión de este concepto matemático. Aquí hay algunas ideas de actividades que pueden ayudar a los estudiantes a consolidar sus conocimientos:
- Identificar el término inicial, la regla de formación y los primeros términos: Proporciona a los estudiantes varias sucesiones y pídeles que identifiquen el primer término (término inicial), determinen la regla que define la sucesión y enumeren los primeros términos. Esto les ayuda a comprender cómo se construye una sucesión y a reconocer patrones.
- Completar sucesiones incompletas: Presenta sucesiones parcialmente completas y pide a los estudiantes que determinen los términos que faltan. Esto les ayuda a aplicar la regla de formación de la sucesión y a desarrollar habilidades de predicción.
- Crear sucesiones propias y describir la regla que las define: Invita a los estudiantes a inventar sus propias sucesiones numéricas, geométricas o aritméticas. Después, pídeles que describan la regla o el patrón que utilizan para generar cada término. Esta actividad fomenta la creatividad y la comprensión profunda de las sucesiones.
- Resolver problemas que involucren sucesiones: Proporciona problemas que requieran el uso de sucesiones para resolverlos, como encontrar el término que sigue en una sucesión dada, calcular la suma de los primeros términos o determinar en qué posición se encuentra un término específico. Estos problemas ayudan a los estudiantes a aplicar los conceptos de sucesiones en situaciones prácticas y a desarrollar habilidades de resolución de problemas.
Al incorporar estas actividades, los estudiantes tendrán la oportunidad de practicar y reforzar sus habilidades con sucesiones, lo que les permitirá comprender mejor este importante concepto matemático.
Tal vez pueda interesarte
- ¿Qué es una sucesión numérica? Para niños
- Numerador y denominador para niños.
- Partes de la división
- ¿Cuál es el valor absoluto y el valor relativo de un número?
Prueba GRATIS de 14 días.
Regístrate hoy mismo para disfrutar de tu prueba gratis de 14 días.
Ahorra hasta el 70% de tu tiempo al planear tus clases.
Obtén acceso inmediato a Planeaciones, Guías, Material y Actividades imprimibles, Juegos educativos multimedia, para Preescolar y Primaria.
Empezar mi prueba gratis