¿Qué significa logaritmo?
Un logaritmo es una función matemática que describe la relación entre una potencia y su base. Los logaritmos son una herramienta matemática poderosa y versátil utilizada en diversas ramas de la ciencia, ingeniería y matemáticas aplicadas. Esta notación matemática, desarrollada por John Napier en el siglo XVI, desbloqueó nuevas formas de resolver problemas complejos relacionados con potenciación y exponenciación. En este artículo, exploraremos en detalle qué son los logaritmos, sus propiedades y cómo se aplican en diferentes contextos.
¿Qué es Logaritmo?
Un logaritmo es una función matemática que describe la relación entre una potencia y su base. La notación general de un logaritmo es la siguiente:
Si tenemos que bx =y, entonces el logaritmo de y en base b se expresa como:
logby=x
Donde:
b es la base del logaritmo.
x es el exponente o potencia a la cual se debe elevar la base b para obtener el número y.
Por ejemplo, si queremos expresar el logaritmo de 9 en base 3, que sabemos que es igual a 2, lo representamos como:
log39=2
Esto significa que 32 =9
Propiedades de los logaritmos
Los logaritmos tienen varias propiedades que facilitan su manipulación y resolución de problemas. A continuación, destacamos algunas de las más importantes:
1. Propiedades Fundamentales
El logaritmo de 1 en cualquier base es siempre igual a 0:
logb1=0
El logaritmo de una base b en la misma base es igual a 1:
logbb=1
2. Producto y Cociente de Logaritmos
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
logb(xy)=logbx+logby
El logaritmo de un cociente es igual a la diferencia de los logaritmos del dividendo y el divisor:
logb( x /y)=logbx-logby
3. Potencia de Logaritmos
El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base:
logb(xy)=y⋅logbx
4. Logaritmo de una Raíz
El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice de la raíz:
log logbn√x=( 1 /n).logbx
Bases especiales de logaritmos
Cuando la base del logaritmo no está explícitamente indicada, se asume que es 10, y los logaritmos se denominan logaritmos decimales. Además, hay una base especial conocida como "e" (aproximadamente 2.718281828) llamada logaritmo natural o neperiano, que tiene aplicaciones especiales en matemáticas y ciencias.
Diferencias entre logaritmo y algoritmo
Es importante destacar la diferencia entre el logaritmo y el algoritmo. El logaritmo es una herramienta matemática que expresa la relación entre potencias y bases, mientras que el algoritmo es un conjunto de instrucciones bien definidas y paso a paso para resolver un problema específico.
Origen del logaritmo
El origen de los logaritmos se remonta al siglo XVI y está estrechamente vinculado con el trabajo de John Napier, un matemático, físico y astrónomo escocés. Napier es considerado el padre de los logaritmos debido a su notable contribución a su desarrollo y popularización.
En 1614, John Napier publicó su obra más importante, titulada "Mirifici Logarithmorum Canonis Descriptio" (Descripción de los Maravillosos Cánones de los Logaritmos). En esta obra, Napier presentó la idea revolucionaria de los logaritmos y su relación con las operaciones de multiplicación y división.
La motivación detrás de la invención de los logaritmos se basó en la necesidad de simplificar los cálculos matemáticos, especialmente en problemas que involucraban operaciones exponenciales y potenciación. Antes del advenimiento de las calculadoras electrónicas y computadoras, los cálculos numéricos eran largos y tediosos, especialmente en astronomía, navegación y otras disciplinas científicas que requerían cálculos extensivos.
Napier se dio cuenta de que había una correlación entre las progresiones aritméticas y geométricas, lo que lo llevó a concebir la idea de los logaritmos. La esencia de su descubrimiento radicaba en que la multiplicación de dos números podía reducirse a la suma de sus logaritmos. Esto permitía realizar la multiplicación mediante una adición directa, lo que simplificaba en gran medida los cálculos.
El trabajo de Napier sentó las bases para el desarrollo posterior de los logaritmos, y su invención fue ampliamente reconocida y aclamada. Su notación original de los logaritmos era algo diferente de la que usamos hoy en día, pero proporcionó la inspiración para que otros matemáticos, como Henry Briggs, mejoraran y extendieran la idea de los logaritmos.
En 1624, Henry Briggs publicó una tabla de logaritmos en base 10, que fue un gran avance en la aplicación práctica de los logaritmos. Estas tablas permitieron a los científicos y matemáticos realizar cálculos complejos de manera más rápida y precisa, y su uso se generalizó rápidamente.
Con el tiempo, los logaritmos se convirtieron en una herramienta esencial para la ciencia, la ingeniería y la navegación, y su importancia continuó creciendo hasta la llegada de las calculadoras mecánicas y, posteriormente, las calculadoras electrónicas y computadoras, que automatizaron los cálculos complejos.
Concluyendo, los logaritmos son una valiosa herramienta matemática que permite resolver problemas relacionados con exponenciación y potenciación de manera más eficiente y simplificada. Sus propiedades fundamentales, junto con sus aplicaciones en diferentes contextos, los convierten en una parte esencial del repertorio matemático y científico.
Características del logaritmo.
Relación entre Exponentes y Potencias: El logaritmo es una función matemática que establece una relación entre un exponente y una potencia y permiten invertir la operación de exponenciación, lo que facilita la resolución de ecuaciones y cálculos logarítmicos.
Simplificación de Operaciones Matemáticas: Una de las principales ventajas de los logaritmos es que simplifican las operaciones matemáticas, especialmente las de multiplicación y división. En lugar de realizar multiplicaciones directamente, se pueden convertir en sumas mediante el uso de logaritmos, lo que facilita los cálculos y permite trabajar con números más manejables.
Propiedades Matemáticas: Los logaritmos tienen una serie de propiedades que los hacen fáciles de manipular y resolver. Algunas de estas propiedades incluyen el logaritmo de 1, el logaritmo de la base en sí misma, el logaritmo de un producto, el logaritmo de un cociente y el logaritmo de una potencia. Estas propiedades son fundamentales para resolver ecuaciones logarítmicas y simplificar expresiones.
Logaritmos en Diferentes Bases: Los logaritmos pueden expresarse en diferentes bases, como base 10 (logaritmos decimales) o base e (logaritmos naturales o neperianos). Cada base tiene sus aplicaciones específicas en diversas ramas de la ciencia y la ingeniería. Los logaritmos en base e son especialmente útiles en problemas que involucran crecimiento y decaimiento exponencial.
Aplicaciones en Ciencias e Ingeniería: Los logaritmos tienen múltiples aplicaciones en diversas disciplinas científicas y de ingeniería. Se utilizan en campos como astronomía, acústica, biología, economía, física, ingeniería eléctrica, entre otros. En la resolución de problemas relacionados con crecimiento, decaimiento, magnitudes astronómicas, señales de audio, escala logarítmica, entre otros, los logaritmos son herramientas esenciales para simplificar y analizar fenómenos complejos.
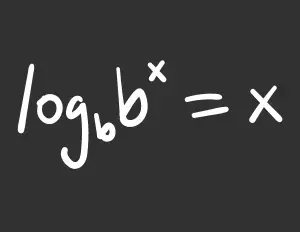
Una logaritmo describe la relación entre una potencia y su base.
Para finalizar, basta recapitular que, un logaritmo es una función matemática que describe la relación entre una potencia y su base. Los logaritmos son una herramienta matemática poderosa y versátil utilizada en diversas ramas de la ciencia, ingeniería y matemáticas aplicadas. Esta notación matemática, desarrollada por John Napier en el siglo XVI, desbloqueó nuevas formas de resolver problemas complejos relacionados con potenciación y exponenciación.
En LEGSA, encontrarás respuestas a varias de las preguntas cotidianas y universales, que nos hacemos todos los días.