¿Qué es el perímetro?
En su esencia más simple, el perímetro es la suma de las longitudes de todos los lados que conforman una figura geométrica plana. En otras palabras, el perímetro es la frontera o contorno que rodea la figura y que determina su extensión en dos dimensiones. Esta medida es especialmente útil cuando se trata de cuantificar la cantidad de material necesario para cercar un terreno, calcular la longitud de un camino o determinar la cantidad de pintura necesaria para cubrir una superficie.
Cuando se trata de figuras geométricas simples, como cuadrados, rectángulos o triángulos, el cálculo del perímetro es directo y se obtiene sumando los lados rectos que los conforman. Sin embargo, en figuras más complejas, como círculos o elipses, el perímetro se calcula utilizando fórmulas específicas que involucran curvas. En todos los casos, el perímetro es una medida fundamental para describir la forma y el tamaño de las figuras geométricas planas.
Unidades de Medida del Perímetro.
La medida del perímetro se expresa en unidades de longitud, y la elección de la unidad depende del sistema de medidas utilizado en un contexto particular. Las unidades de longitud más comunes son centímetros (cm), metros (m), pulgadas (in) y pies (ft). Cada una de estas unidades tiene su propio propósito y escala de medida:
Centímetros (cm): El centímetro es una unidad de medida del sistema métrico y se utiliza comúnmente en todo el mundo. Es una unidad pequeña que se utiliza para medir longitudes más cortas, como las de objetos cotidianos o dimensiones de figuras geométricas pequeñas.
Metros (m): El metro es la unidad fundamental del sistema métrico y se utiliza ampliamente para medir longitudes más grandes, como las de habitaciones, edificios, terrenos y distancias en carreteras.
Pulgadas (in): La pulgada es una unidad de medida del sistema imperial que se utiliza en países como los Estados Unidos y el Reino Unido. Se usa comúnmente para medir longitudes más pequeñas y precisas, como las de herramientas o materiales de construcción.
Pies (ft): El pie es otra unidad del sistema imperial utilizada en países como los Estados Unidos. Se compone de 12 pulgadas y se usa para medir longitudes de objetos más grandes, como las de una habitación o parcela de terreno.
Es importante asegurarse de que todas las dimensiones estén en la misma unidad de medida antes de calcular el perímetro, ya que la suma de longitudes en diferentes unidades podría dar como resultado un valor incorrecto. El uso adecuado de las unidades de medida es vital para lograr mediciones precisas y poder aplicar entonces, el perímetro de manera efectiva en diversos contextos, desde la construcción y la arquitectura hasta la resolución de problemas matemáticos.
¿Cómo Calcular el Perímetro?
El cálculo del perímetro de una figura geométrica depende de la forma específica de la figura. Aquí hay algunas fórmulas clave para calcular el perímetro de algunas figuras geométricas comunes:
Cuadrado: El perímetro de un cuadrado se obtiene multiplicando la longitud de uno de sus lados por 4. La fórmula es P = 4 × L, donde "P" es el perímetro y "L" es la longitud de uno de los lados.
Rectángulo: El perímetro de un rectángulo se calcula sumando el doble de su longitud y el doble de su anchura. La fórmula es P = 2 × (longitud + anchura).
Círculo: Para un círculo, el perímetro se llama circunferencia y se calcula mediante la fórmula C = 2πr, donde "C" es la circunferencia, "π" es el valor de pi (aproximadamente 3.14159), y "r" es el radio del círculo.
Polígonos Regulares: Para polígonos regulares, aquellos con todos los lados y ángulos iguales, el perímetro se calcula multiplicando el número de lados por la longitud de uno de los lados. Es decir, P = número de lados × longitud del lado.
Perímetro de Figuras Compuestas:
Cuando nos enfrentamos a una figura geométrica compuesta, es decir, una figura que está formada por varias formas geométricas individuales, el cálculo del perímetro se vuelve un poco más complejo pero igualmente factible. La clave aquí es descomponer la figura compuesta en sus componentes simples, calcular el perímetro de cada una de estas partes por separado y, finalmente, sumar estos valores para obtener el perímetro total de la figura compuesta. Este enfoque se aplica a situaciones en las que una figura, como un jardín con senderos o un edificio con extensiones irregulares, se compone de múltiples formas geométricas, como rectángulos, triángulos y círculos. El cálculo preciso de los perímetros individuales es esencial para determinar la cantidad de material necesario o para establecer límites claros en contextos de diseño y construcción.
Unidades Mixtas:
Cuando se calcula el perímetro, es fundamental garantizar que todas las dimensiones involucradas estén en la misma unidad de medida antes de realizar cualquier operación matemática. Si las dimensiones se expresan en unidades mixtas, es decir, diferentes unidades de longitud, es necesario convertirlas a una unidad común antes de sumarlas para calcular el perímetro correctamente. Por ejemplo, si estamos midiendo un terreno y tenemos una longitud en metros y otra en pies, debemos convertir una de ellas para que ambas estén en la misma unidad, ya sea metros o pies, antes de sumarlas. La conversión precisa de unidades es esencial para evitar errores en los cálculos del perímetro y garantizar mediciones precisas en situaciones del mundo real.
Escala:
Cambiar la escala de una figura, ya sea haciendo que sea más grande o más pequeña, tiene un efecto directo en su perímetro. Cuando se escala una figura, todos sus lados y dimensiones se multiplican por el mismo factor de escala. Por lo tanto, el perímetro de la figura escalada será proporcional al factor de escala aplicado. Si la figura se hace más grande, su perímetro aumentará en proporción; si se hace más pequeña, el perímetro disminuirá en proporción. Esta propiedad es esencial en áreas como la arquitectura y el diseño gráfico, donde se deben adaptar dimensiones y tamaños de figuras a diferentes escalas sin perder la precisión en el cálculo del perímetro. El conocimiento de cómo la escala afecta al perímetro es crucial para lograr resultados precisos y proporcionados en el diseño y la representación de objetos y estructuras.
Perímetro en Contextos Avanzados
En contextos avanzados de geometría y cálculo, el cálculo del perímetro se extiende más allá de las figuras geométricas simples y se aplica a formas más complejas. Una técnica matemática utilizada en este contexto es la integral de línea. La integral de línea es una herramienta poderosa que permite calcular el perímetro de curvas irregulares y figuras que no pueden descomponerse fácilmente en segmentos rectos o curvas simples.
La integral de línea se basa en la descomposición de una curva en segmentos infinitesimales, a menudo utilizando coordenadas paramétricas. Cada segmento se analiza individualmente, y mediante un proceso de integración, se suma la longitud de todos estos segmentos para obtener el perímetro total de la figura. Esta técnica se aplica en campos como la geometría diferencial, donde se estudian curvas y superficies en detalle, así como en problemas de física y análisis matemático avanzado.
Relación con el Área
Aunque el perímetro y el área están relacionados en el sentido de que ambos conceptos se utilizan para cuantificar características de una figura geométrica, son dos medidas distintas con propósitos diferentes. La diferencia clave radica en lo que cada uno representa.
El área de una figura se refiere a la cantidad de superficie encerrada por los límites de la figura. Es decir, el área mide la extensión de la región que ocupa la figura dentro de esos límites. Por otro lado, el perímetro se refiere exclusivamente a la longitud de los límites o el contorno de la figura, sin tener en cuenta el espacio interior que encierra.
La relación entre el área y el perímetro se puede ilustrar en el caso de un rectángulo. A medida que se aumenta la longitud de uno de los lados de un rectángulo mientras se mantiene constante la longitud del otro lado, el área aumenta, pero el perímetro también aumenta. Sin embargo, estos dos conceptos pueden variar independientemente entre sí. En otras palabras, es posible encontrar figuras con el mismo perímetro pero áreas diferentes y viceversa.
Esta distinción es fundamental en problemas de diseño, construcción y optimización, donde a menudo se busca maximizar o minimizar una de estas medidas mientras se mantiene la otra constante. La relación entre el área y el perímetro es un tema central en la geometría y el cálculo, y su comprensión es esencial para abordar una amplia variedad de problemas matemáticos y de ingeniería.
Perímetro en el Mundo Real
La comprensión del perímetro es fundamental en numerosos aspectos de la vida cotidiana y en diversas disciplinas. Algunos ejemplos de su aplicación incluyen:
Arquitectura y Construcción: Los arquitectos utilizan el cálculo del perímetro para determinar la cantidad de material necesario para cercar un terreno o para diseñar estructuras con dimensiones específicas.
Agricultura: En la agricultura, calcular el perímetro de un campo es esencial para planificar la instalación de cercas o para calcular la cantidad de alambre necesario para delimitar áreas de cultivo.
Geografía y Topografía: En la cartografía y la topografía, el cálculo del perímetro es importante para medir la longitud de las costas de un país o la longitud de fronteras entre regiones geográficas.
Educación Matemática: En la enseñanza de las matemáticas, el concepto de perímetro se utiliza para introducir a los estudiantes a la geometría y para enseñarles cómo calcular la longitud de los lados de diferentes figuras geométricas.
En sintesís, el perímetro es una medida fundamental en geometría que representa la longitud total de los bordes de una figura geométrica plana. Se calcula sumando las longitudes de todos los lados que componen la figura, ya sean rectos o curvos. Este concepto es ampliamente utilizado en numerosos campos, desde la construcción y la arquitectura hasta la topografía y la educación matemática. Además, el perímetro puede aplicarse en contextos avanzados mediante técnicas como la integral de línea, y está relacionado pero es diferente del área, ya que mientras el área mide la superficie encerrada por una figura, el perímetro mide la longitud de su contorno.
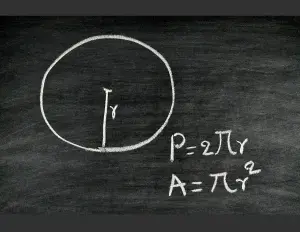
El perímetro es la suma de las longitudes de todos los lados que conforman una figura geométrica plana.
Características de el perímetro.
Longitud de Contorno: El perímetro mide la longitud total del contorno o borde de una figura geométrica plana. Es la suma de las longitudes de todos los lados que conforman la figura.
Unidades de Medida: Se expresa en unidades de longitud, como centímetros, metros, pulgadas o pies, dependiendo del sistema de medidas utilizado.
Aplicación en el Mundo Real: El cálculo del perímetro es fundamental en situaciones prácticas, como la construcción, la topografía, la agricultura y la geometría, donde se utiliza para medir terrenos, delimitar áreas, calcular la cantidad de material necesario y resolver problemas matemáticos.
Descomposición de Figuras Compuestas: Cuando una figura está compuesta por varias formas geométricas, se puede calcular el perímetro de cada forma por separado y luego sumarlos para encontrar el perímetro total de la figura compuesta.
Relación con el Área: Aunque relacionado, el perímetro y el área son conceptos diferentes. El área mide la superficie encerrada por una figura, mientras que el perímetro se centra en la longitud de su contorno. Ambos conceptos tienen aplicaciones específicas en distintos contextos matemáticos y prácticos.
5 ejemplos de el perímetro.
Perímetro de un Cuadrado: Supongamos que tienes un cuadrado con lados de 5 centímetros de longitud. Para calcular su perímetro, simplemente sumas los cuatro lados: P = 4 × 5 cm = 20 cm.
Perímetro de un Rectángulo: Imagina un rectángulo con una longitud de 8 metros y una anchura de 4 metros. El perímetro se calcula sumando dos veces la longitud y dos veces la anchura: P = 2 × (8 m + 4 m) = 24 metros.
Perímetro de un Círculo: Para encontrar el perímetro de un círculo, también conocido como circunferencia, debes usar la fórmula C = 2πr, donde "π" es el valor de pi (aproximadamente 3.14159) y "r" es el radio del círculo. Si el radio es de 10 cm, entonces: C = 2 × 3.14159 × 10 cm ≈ 62.83 cm.
Perímetro de un Triángulo: Supongamos que tienes un triángulo con lados de 7 cm, 10 cm y 15 cm. El perímetro se obtiene sumando las longitudes de los tres lados: P = 7 cm + 10 cm + 15 cm = 32 cm.
Perímetro de un Polígono Irregular: Si tienes un polígono irregular con lados de longitudes diferentes, como 6 cm, 8 cm, 5 cm, 9 cm y 7 cm, simplemente sumas todas las longitudes de los lados para encontrar el perímetro total: P = 6 cm + 8 cm + 5 cm + 9 cm + 7 cm = 35 cm.
Para finalizar, basta recapitular que, en su esencia más simple, el perímetro es la suma de las longitudes de todos los lados que conforman una figura geométrica plana. En otras palabras, el perímetro es la frontera o contorno que rodea la figura y que determina su extensión en dos dimensiones. Esta medida es especialmente útil cuando se trata de cuantificar la cantidad de material necesario para cercar un terreno, calcular la longitud de un camino o determinar la cantidad de pintura necesaria para cubrir una superficie.
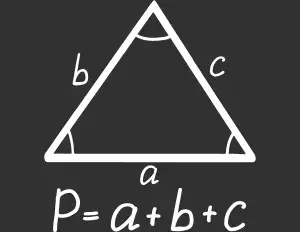
Un ejemplo de perímetro es el del triángulo.
En LEGSA, encontrarás respuestas a varias de las preguntas cotidianas y universales, que nos hacemos todos los días.